2022-09-10

135. AtCoder参加記録（AtCoder Beginner Contest 268）

プログラミング AtCoder

38回参加でレート 1377 です。

今回はパフォーマンス 1453 です。

ABCDを通して、EFGExは未解答です。Dで3ペナ。

各問題の思考過程など。

A

問題

1分13秒。

HashSet に全部突っ込んで要素数を出す。

ACコード

B

問題

1分13秒。

C# なら、T.StartsWith(S) で判定できる。

ACコード

C

問題

9分23秒。

C問題にしては急に難しいので、落ち着いて問題を読む。1回ずつテーブルを回してその時の「喜ぶ人数」を $O(1)$ で求めるような形にしたい。
「料理 $i$ と正しいインデックスの距離的なもの」は、ざっくり $d_i = p_i - i$ と計算できる（この式は負の方向を考えていない）。
この「距離的なもの」はテーブルを 1 回動かすごとに 1 ずつ増加する。
$d_i = j$ であるような $i$ の種類数を $c_j$ とすると、求める答えは $c_{N-1} + c_{0} + c_{1}$ と表現できる。
3. の考察から $c$ は 1 つずつ回転していくような動きをする。
以上より、初期状態での $c$ を求めた後、インデックス 0 とみなす点を全探索すればよい。

ACコード

D

問題

初回提出 24分45秒、2回目提出 2分59秒、3回目提出 3分4秒、4回目提出(AC) 16分46秒。

$X$ が $T$ のいずれかと一致しているかは HashSet を使えば $O(1)$ で求められる。
連結順は順列全探索で決定できる。 $N \le 8$ という制約なので、ここからも順列全探索が想定されていることが分かる。
連結順が求まれば、後はアンダーバーを追加して一致を見れば良いだけ？と考えたが、どこかにアンダーバーを2つ以上繋げないと $X$ を作れないテストケースは容易にできることに気付く。
ということは、アンダーバーの数についても、それぞれの位置について全探索する必要がありそう…。 $|X| \le 16$ という条件なので、計算量は問題ない。
まとめると、
1. $T$ を全て HashSet に突っ込む
2. $S$ の連結順を順列全探索する
3. 連結に用いるアンダーバーの数を $|X| \le 16$ という制約のもとDFS全探索する
4. $X$ が HashSet に含まれていなければそれを出力する
5. 最後まで探索して答えが見つからなければ -1 を出力する
実装が重すぎる…と思いつつ書き上げると、入力例 1 でいきなり RE する。 $N = 1$ のときのみ例外処理で判定する。
これで入力例は合ったので投げてみる → 5WA
問題文を読み直すと、 $|X| \ge 3$ という条件があった。は？と思いつつ、DFS全探索にこの条件を組み込む → 7WA（うちサンプルで1WA）
参照していた変数がおかしかったので直す。ついでに $N=1$ のときの $|X| \ge 3$ 条件が抜けていたので入れる → 3WA
流石にこれは何かバグらせているので、一旦落ち着いてじっくりデバッグする。怪しいのはDFS全探索の部分。見てみると、アンダーバーの数の全探索について、最初のアンダーバーの数だけ 1 or 2 でしか探索できていなかった（ダメすぎる）。
これを修正して無事AC。

ACコード

E

問題

解けず。

Cの類題。ただ、考え方のベースはCと同じで良さそうに思える。
正しいインデックスとの距離的なもの $c$ を考える。テーブルが1回動くと、だいたいインデックス $N / 2$ を境界に、それより前のものは不満度が 1 加算され、後のものは不満度が 1 減算される。
「不満度加算集合」「不満度減算集合」を管理しつつ、1 つずつ状況を変化させれば良さそう。1回の変化で、それぞれの集合から1つずつ要素が出入りするので、スコア計算もそれで差分を取ればよい。
入力例 3 が合わず撃沈…。実装ミスのようです。

F, G, Ex

見てないです。

実装重すぎ回。Cが割とすぐ解法見えたのは良かったですが（遅延セグ木使おうかと血迷っていたけど留まった）、DでDFS全探索をバグらせたのは普通によくないので、今まで雰囲気で書いてきていたのですが、これを機にちゃんと見直してみようと思います。

ある程度しっかり方針立ててから実装に入れたのは良い成長。でも、Eバグらせたのは悔しすぎる～～。

2022-09-05

134. AtCoder参加記録（AtCoder Regular Contest 147）

プログラミング AtCoder

37回参加でレート 1369 です。

今回はパフォーマンス 1319 です。

ABを通して、CDEFは未解答です。Aで2ペナ、Bで1ペナ。

各問題の思考過程など。

A

問題

初回提出9分47秒、そこから2回目提出4分20秒、Bから戻ってACまで18分59秒。

操作回数は一定らしいので愚直にシミュレートすればよさそう。
最大値・最小値を取り出しつつリストを更新したいので、MultiSetを使ってみる → 2ケースTLE
計算量的にはたぶん間に合っているので定数倍っぽい。PriorityQueue でも解けるしこっちの方が軽いので、こちらにしてみる → 最終ケースのみTLE（意地悪…）
これで間に合わないなら何らかの数学的性質を使う？ユークリッド互除法的な操作だとは思うけど、どうしたらいいのか分からない…Bへ移る。
Bから戻ってきて改めて紙上で操作してみると、1回の操作で計算後の値は必ず次の最小値になると気付く。
昇順にリストが並ぶと考えれば先頭・末尾のみ操作する形になるので、Deque が使える。対数時間が定数時間に落ちるので、これで通らないか賭けてみる。普通に通って唖然…。

C++だと 2. の解法で通ったらしい……

ACコード

B

問題

Aを諦めてから初回提出21分21秒、そこからACまで16分27秒。

操作回数には十分余裕がありそうなので、この制約は無いものとして考える
各要素について正しい位置のインデックスと偶奇が一致していない場合は操作Aを行う必要がある。1の場所から順に見て、偶奇が一致していなければ操作Aを1度行ってから、あとは操作Bで正しい場所へ持っていく → 大半WA
少し考えると、 $P = (3, 1, 5, 4, 2)$ のようなケースでうまくいかないことが分かった。このケースは $1$ と $2$ について操作Aが必要だが、本来は1度で済むところが 2. のアルゴリズムだと2度以上行ってしまう。これは、偶奇の一致してない要素が隣り合っていないため上手く行ってない。
偶奇が一致してない場所は必ず偶数箇所あるので、一致してない要素を全部先頭側へ（操作Bで）持っていき、操作Aを奇数番目に対して順に行い偶奇を一致させた後、操作Bで正しい場所へ持っていけばよい。

ACコード

C, D, E

それぞれ10分ほど考えたが、解決の糸口になりそうなものは何も浮かばず。

F

見てないです。

A、なんとなくC++だと通る解法なのでは…と思っていましたが、案の定で…割と萎えました。

最近仕事が忙しくあまり問題を解いていなかったので、レートが下がるのは甘んじて受け入れ、来週また頑張ります。

2022-09-03

133. AtCoder参加記録（AtCoder Beginner Contest 267）

プログラミング AtCoder

36回参加でレート 1374 です。

今回はパフォーマンス 1265 です。

ABCDを通して、FGExは未解答です。Eは通せず。Aで1ペナ…。

各問題の思考過程など。

A

問題

初回提出1分48秒、そこからACまで53秒。

配列に各文字列を入れてインデックスとの差を出力しました。Friday をコピペしたときに何故か空白が入っていて1ペナ…なんで…。

ACコード

B

問題

8分35秒。

書かれている通りにやるだけですが、まあまあ面倒くさかったです。

ACコード

C

問題

7分43秒。正直、Dより難しかったです。

区間の長さが決まっているので、1つずつずらして差分を見る方針が良さそう
計算式を考慮すると、たとえば始点が $i \rightarrow i + 1$ へずれたなら差分は $M \times A_{i+1} - \sum_{j = i}^{i+M-1} A_j$ になる
引き算部分は累積和を持っておけば $O(1)$ で求められるので、始点全探索で $O(N)$ となる

ACコード

D

問題

4分59秒。

Cとほぼ同じ問題で、連続という条件が外れたバージョン
制約を見ると $O(N^2)$ が通るようになっている。一項ずつ見ていって最適なものだけ残す感じにしたいので、DPを考える。
$dp[i,j] := (A_{i} まで見た時の、長さ j の部分列に対する与式の最大値)$ とすればOK。答えは $dp[N,M]$ 。

ACコード

E

問題

初回提出38分36秒。通せず。

この手のはとりあえず操作の反対側から考えてみるが、今回は逆に難しくなりそうなので素直に前から削除していくことに
各頂点に削除コストがあるとして、ある頂点を削除するとその頂点と隣接する頂点の削除コストが減っていくようなイメージ
貪欲アルゴリズムは思いつかないので、解の二分探索を考える。削除コストを MultiSet に入れて、削除可能な頂点を削除コストの大きい順に消して行ってみる。
実装がめちゃくちゃ重くなったが、サンプルは通ったし、 $O(N(\log N)(\log K))$ （ただし $K$ は解の存在しうる最大値）で実行時間制限4秒なので、まぁ大丈夫かな…と出してみるが、WAもTLEも出てボロボロ。
TLEだけならまだしも、WAが出ている意味がわからず、諦めてしまう

解説を読むと方針は普通に合っていて、何処かに実装ミスがあったのだと思われます。あと MultiSet が予想以上に重かったです。

（以下、Upsolve）

本番で提出したコードですが、MultiSet に加えて隣接点を管理していた nexts 変数のディープコピーがボトルネックになっていました。また、WAは二分探索の上限設定ミス（削除コストは隣接点の和を取ることを忘れていて $10^9$ にしていた）だったので、もう少しちゃんと考えれば通せていた問題でした。最近悪い意味で諦めが良くてダメですね…。

解の二分探索での上限は何も考えずに $10^{18}$ とかにしてしまって良い気がしてきました。

Upsolveコード

F

問題

解けず。10分ほど考えましたが何も浮かびませんでした。

G, Ex

見てないです。

Aのペナは事故っぽいので仕方ないですが、E通せなかったのは悔しいですね…。

最近よくあるパターンで、考察段階で「実装重そう」と思っていざ書き始めるとちょいちょい要素の欠落があり、結果的に激重実装となりバグらせる…というものでした。考察時点で重いと感じるのであれば、もう少しシンプルに解決できないか立ち止まって考える練習が必要そうです。

2022-08-27

132. AtCoder参加記録（AtCoder Beginner Contest 266）

プログラミング AtCoder

35回参加でレート 1386 です。

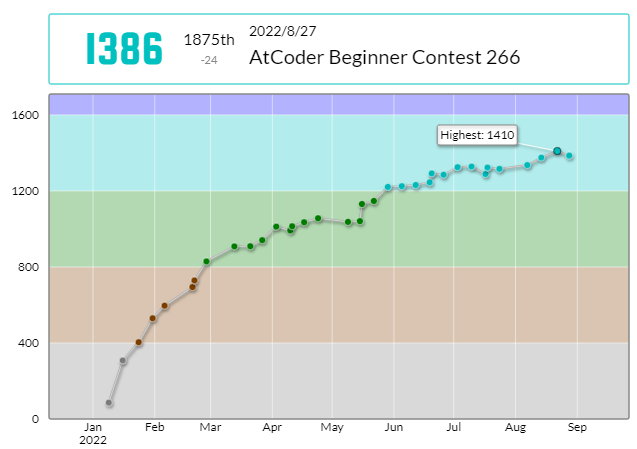
今回はパフォーマンス 1149 です。

ABCDを通して、EFGExは未解答です。

各問題の思考過程など。

A

問題

56秒。やるだけ。

ACコード

B

問題

3分38秒。

$x \equiv N \pmod{998244353}$ となる条件を満たす数を見つければよいので、 $N$ を初期値として適当に足したり引いたりするようにしました。雑に書きましたが、思ったより重くてちょっと反省。

ACコード

C

問題

11分13秒。

問題を読んでガチガチの幾何問が来たことに驚きました。

3点で三角形を作ったときもう1点が三角形内部にあるとダメなような気がする（未証明、直感）
三角形の外部・内部判定ってたしか外積で出来たような…。分からんのでググる
ググって出てきた三角形の内部判定をそのまま書き下し、点の組み合わせ全てを試す感じに

ACコード

D

問題

9分45秒。

移動速度の記述理解にやや時間が掛かったが、要するに1つ隣へ行くかその場に留まるか、ということか
同じ時刻・同じ場所においてスコアが最大となる手が明らかに最適なので、これだけ残して探索すればよい。ここからDPっぽさを感じる。
$T_i \le 10^5$ で場所が5箇所しかないから行ける。

ACコード

E

問題

解けず。最初そもそも問題を誤読していた…。

色々よく分からない考察をする（何考えてたか覚えてない…）
1回だけサイコロを振るなら出目の期待値は 3.5 なので、3以下なら振り直すのがよい
じゃあ出目が3以下なら振り直し続ければよいのでは？と考えるが入力例3が合わない
何もわからないのでFへ…

F

問題

解けず。Eよりこちらの方が見込みありましたが、Eで気持ちが落ちていて最後まで詰めきれなかった感が強いです。

木に1本だけ辺が追加されたグラフなので、閉路的なものが1つあるグラフになる（ここで何故か閉路を構成する頂点が3つだけだと思い込む）
閉路を経由する必要があるときだけ単純パスは一意に定まらない
閉路を経由する必要が無いのは、閉路を構成する頂点で最も近いものが等しいペアの場合
DFS・BFSをゴチャゴチャやって閉路を構成する頂点集合を特定し、そこに含まれる各頂点から全頂点への距離を出しておけば、クエリに $O(1)$ で答えられる（閉路を構成するのが3頂点だけだと思い込んでおり、これで間に合うと考えていた）
かなりの時間を掛けて実装し、入力例1は合うが2が合わない。デバッグすると閉路を構成する頂点集合は3つより多い…。少し考えて、3つに限らないことに気付く。
今の実装を少し変えて何とかならないか考えたが、明らかにTLEするしもう時間も無いので諦め

G, Ex

見てないです。

Dまでのスピードは良かったですが、E・Fともに考察で詰めきれず迷走した感が強かったです。最近あまりAtCoderの問題を解いてなかったので（それ以外の問題を解いていた）、なんだか気持ちが入り切らなかったというのもあるかもです。

ABCでは3ヶ月ぶりの緑パフォを取ってしまいました。ちょっと詰まったら途端に思考が鈍るの改善していきたいですね…。

2022-08-21

131. AtCoder参加記録（AtCoder Beginner Contest 265）

プログラミング AtCoder

34回参加でレート 1410 です。

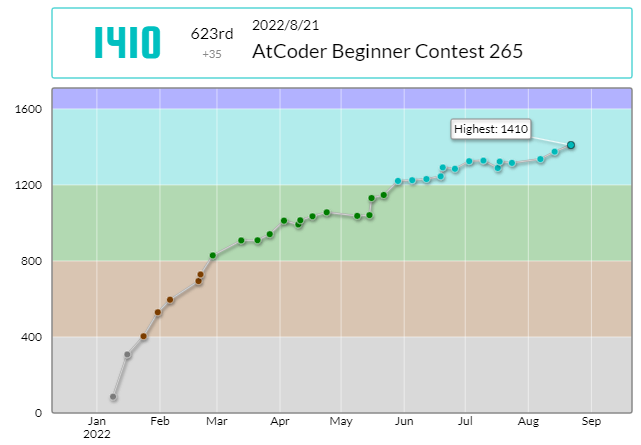
今回はパフォーマンス 1680 です。

ABCDEを通して、FGExは未解答です。Cで1ペナ、Dで1ペナ。

各問題の思考過程など。

A

問題

2分7秒。

パッと思いつかなかったので全探索しました…

ACコード

B

問題

4分38秒。

書かれている通りにやるだけ。持ち時間の消費タイミング、移動可能判定のタイミングなどに注意しつつ書けばOK。

ACコード

C

問題

初回提出6分10秒、そこからACまで1分16秒。

あるマスにいるとき取れる行動は1つだけなので、以前訪れたマスに再訪した場合は無限ループになります。よって、状態は $O(HW)$ しか無いので普通にシミュレーションすれば間に合います。

if に else を付けるのをサボってバグらせてしまい、悲しい1ペナ。かなり痛い…。

ACコード

D

問題

初回提出8分37秒、そこからACまで8分11秒。

ちょっとややこしいので入力例1を書いてみる。区間和が $P + Q + R$ になるような場所を見つけるのが必要なのか。
区間和なので累積和がすぐ想起される。
$x$ が決まれば、 $y$ は $x$ から $y-1$ の区間和が $P$ になるところ、 $z$ は $x$ から $z-1$ の区間和が $P+Q$ になるところ、 $w$ は $x$ から $w - 1$ の区間和が $P+Q+R$ になるところを求めればよい。一見ややこしいが、要するに「累積和に対して二分探索」を3回並列でやるだけ。これで $O(N \log N)$ なのでOK。
添字バグで1ペナ。やたら時間を取られつつ修正…。

なんでこんなに時間掛かったんだろう…という感じでした。添字バグは普通に実力不足。

ACコード

E

問題

37分11秒。正しい方針に辿り着くまでかなり時間を要しましたが、そこからは早かったです。

愚直解は $O(3^N)$ なので当然無理。
全通りから障害物を通るルートだけ引く？と考える。操作1～3をそれぞれ何回行うのか、を全探索すれば $O(N^3)$ になるので、計算量的にこの操作が想定解に含まれてる気がする。
各操作回数が決まった状態で辿り着く座標は、操作順序に依存しない。ある操作回数で障害物に辿り着いた場合、そこまでの通り数は次のステップに加算しないような処理になれば嬉しい… → ここからDPに発想が行き始める
少しずつ操作回数を増やすようなDPなので、（全操作回数, 操作1の回数, 操作2の回数, 操作3の回数）という状態が必要そう…。これは流石に実行時間制限3秒でも無理では？
操作3の回数は、全操作回数から他の操作回数の和を引けばよかった。じゃあこれでいいか。
ある座標に障害物が存在するかは、座標値を上手く64ビット整数に押し込むことで HashSet によって $O(1)$ で判定できる。
$dp[i,j,k] = (全i回操作し、操作1をj回、操作2をk回行うときの障害物を経由しない通り数)$
という定義になる。

ACコード

F

問題

解けず。

Eまでに時間を掛けすぎた感覚はあったので、ひとまず順位表を見ると全然通されてない…。ということは、だいぶ難しい問題なのだなと覚悟しました。

チェビシェフ距離に変換して…みたいなことを考えていましたが、 $N$ 次元なので無理では、となり断念。何の方針も立たなかったので10分くらいで諦めました。

G

問題

Fよりはこちらの方が取っつきやすさはありました…が、遅延評価セグメント木を使ってもちょっと無理そうな操作だったので、他に打つ手が無く諦めました。

Ex

見てないです。

今日もペナが勿体ない日でした…。これだけでパフォーマンス100以上は落としています。Eがもう少し早く解けてればなぁ、という気持ちですが、実力相応という感じが強いです。

とりあえず水色の折り返し地点であるレート1400に乗りました。アルゴリズムは未だに最高パフォーマンスが1701（この前初参加したヒューリスティック（1744）の方が高い）なので、ここから先は厳しい戦いになりそうな予感がします。

Gを当てられるようになったら最高レート自体は青に届くと思いますが、たぶん維持が難しいので、ひとまずEまでを素早く正確に解くこと・Fを30%くらい通せるようになることを当面の目標としたいです（精選上級編がつらかったのもあります）。

青diff問題をひたすら解くような感じで頑張っていこうと思います。

2022-08-16

130. AtCoder参加記録（AtCoder Heuristic Contest 013）

プログラミング AtCoder AHC

暫定テスト142位、215,674点です。システムテストでは143位、1744 perf でした。

AtCoder Heuristic Contest に初参加しました。

マラソンは初めてでしたが、コンテスト中にブレイクスルーがいくつかあってとても楽しかったです。また、自分の解法だと22万点くらいが限界だと思うので、30万点超えている人がどういう方針で解いているのかとても興味深かったです。

解法
日記
- 8/9
- 8/10
- 8/11
- 8/12
- 8/13
- 8/14
- 8/15
- 8/16
やっておけばよかったこと
- 自動テスト
- リファクタリング

2022-08-13

129. AtCoder参加記録（AtCoder Beginner Contest 264）

プログラミング AtCoder

33回参加でレート 1375 です。

今回はパフォーマンス 1668 です。

ABCDEを通して、GExは未解答です。Fは通せず。

各問題の思考過程など。

A

問題

1分18秒。

C# だと S.Skip(L - 1).Take(R - L + 1) でいいです。

ACコード

B

問題

4分41秒。

問題を開いた瞬間に目がやられました。いまいちどう表現して良いのか分からない盤面だったので、とりあえず思いついた書き方で構築しました。

Bはこうした pic.twitter.com/z3mWB0mxbc
— イバコ (@ibako_piyo) 2022年8月13日

真ん中からのチェビシェフ距離だったらしい。なるほど…。

ACコード

C

問題

8分6秒。

ちょっと考えて「うーん、全探索しか無さそう」となり、制約を見て「bit全探索か」となりました。微妙に間に合うのか心配でしたが、これ以外思いつかなかったので細かい実装方針を詰めてから書きました。PopCount初めて使ったかも。

ACコード

D

問題

4分15秒。

バブルソートするだけでは…となり、そのとおりに書きました。

ACコード

E

問題

初回提出19分19秒、そこからACまで3分43秒。

こういう系は逆から考えるのが定石。逆からなら Union-Find やるだけで良いな、と方針を決定
あとは丁寧に実装する

何故か2WA出て頭を抱えましたが、同一グループに属しているかの判定が一箇所抜けていました。これだけで70近くパフォを落としているので、だいぶ勿体なかったです。

ACコード

F

問題

初回提出48分58秒。解けず。

必ず $H + W - 2$ 手で終わる、右か下かを選択して進めるということでDPっぽい。
何が状態になるのか考えると、以下の5要素で良さそう？
1. どの行にいるのか
2. どの列にいるのか
3. 0 と 1 どちらのマスを通っているのか
4. 現在いる行が反転されているか
5. 現在いる列が反転されているか
状態数は $2^3HW$ なのでとりあえず間に合いそう。後は遷移を丁寧に考えれば良いかな…とそれっぽいものを書き、とりあえずサンプルは合うようになった。投げてみると半分以上 WA。
入力例 1 のDPテーブルを見ながらデバッグ・修正したが、結局 WA の数は変わらず。

（以下、Upsolve）

冷静に考えると、遷移が一部間違っていることを理解した…。どういう状態を持っているのかちゃんと認識できておらず、混乱したコードを書いていたのが敗因。

これは通せた問題だったので勿体なかったです。

Upsolveコード

G

Fの遷移を考えていてよく分からなくなったので、こちらも見ました。全然解けそうになかったので5分くらいで見るのをやめました。

Ex

見てないです。

Eのペナがとても勿体なかったですが、とりあえず久々の青パフォで嬉しかったです。F解きたかったなぁ。